例1:从36位同学中选取2人参加竞赛,问共有多少种不同的选法?
例2:甲、乙、丙三个人到旅店住店,旅店里只有三个房间,恰好每个房间住一个人,问一共有多少种不同的住法。
我们发现从36人中选取2人,结果与选取的顺序无关,则为组合,记为C,满足的情况数为![]() ,三个房间按照三人排序的不同入住,结果也不同,那么这就是说结果与选取的顺序有关,则为排列,记为A,满足的情况数为
,三个房间按照三人排序的不同入住,结果也不同,那么这就是说结果与选取的顺序有关,则为排列,记为A,满足的情况数为![]() ,在此,我们做一下总结,排列与顺序有关,而组合与顺序无关。
,在此,我们做一下总结,排列与顺序有关,而组合与顺序无关。
3.2加法和乘法原理
例3:从A地到B地,可以乘坐高铁或飞机或大巴,则从A地到B地共有多少种不同的交通方式?
例4:制造一件零件需E、F共2道工序。完成E有3种方法,完成F有4种方法,则完成此零件共有几种制造方法?
在这里我们通过2道例题来说明加法和乘法两个原理,例3中我们无论乘坐高铁或飞机或大巴均可独立完成从A地到B地的事件,因此我们把从A到B分成了三类,每一类均可独立完成,总的不同的交通方式等于各类的满足情况数之和;例4中我们发现完成这个零件需要2道工序,每道工序均不能独立完成该事件,则这种情况我们称为分步,总的情况数等于每一步情况数相乘。
3.3基本公式的计算

四.方法与技巧
排列组合类的题,我们除了需要掌握相关的概念,能够区分出排列与组合的区别以及掌握排列组合的基本公式外,我们还需要掌握一些解题的方法和技巧,只有这样才能应对灵活多变的考题,做到知识点了然于胸。下面对常见的方法和技巧进行讲解。
4.1捆绑法
例5:ABCDE共5人排成一行,要求AB两人必须相邻,则共有多少种排列方式?
我们发现这是一道排列的题目,与顺序有关,题目要求AB相邻,这样我们可以把AB捆绑在一起看成一个元素,则将总的四个元素进行排列![]() ,然后AB的内部需要重排,即
,然后AB的内部需要重排,即![]() ,整个过程属于分步,则总的排列方式等于
,整个过程属于分步,则总的排列方式等于![]() 。针对题目中出现相邻要求时,优先考虑捆绑法。
。针对题目中出现相邻要求时,优先考虑捆绑法。
4.2插空法
例6:ABCDE共5人排成一行,要求AB两人不相邻,则共有多少种排列方式?
首先判断该题属于排列,与顺序有关,那么要求AB不相邻,这时候我们可以优先将CDE三人进行重排,即![]() 然后CDE形成了4个空,从这四个空中选出2个分别放入AB即可实现AB不相邻的要求,即
然后CDE形成了4个空,从这四个空中选出2个分别放入AB即可实现AB不相邻的要求,即![]() ,那么总的排列方式:
,那么总的排列方式:![]() 。针对元素要求不相邻的题目,我们优先安排没有要求的元素,然后将要求不相邻的元素进行插空即可。
。针对元素要求不相邻的题目,我们优先安排没有要求的元素,然后将要求不相邻的元素进行插空即可。
4.3隔板法
例7:把8个相同的苹果分给4个人,要求每人至少分得一个苹果,则共有多少种的分配方法?
题目出现了相同元素,并且出现了至少分一个的字眼的分配问题的时候,我们考虑是隔板法,这里直接将公式给出:将n个相同元素分给m个人,要求每人至少分得1个元素,则总的分配方式为![]() ,因此该题的分配方式为
,因此该题的分配方式为![]() 。
。
4.4环形排列
例8:3个小朋友围着一个圆桌吃饭,问共有多少种不同的安排方法?
本题是环形排列问题,与顺序有关,我们知道如果三个人直线排列,则共有种排列方式,那么环形排列有什么不同吗?我们可以看下图,我们发现图中的三种排列方式在环形中其实是一种排列方式,因此,将n个不同元素进行直线型排列的情况数是其环形排列情况数的n倍,即n个不同元素进行环形排列的总的排列数为:![]() ,因此三人圆桌吃饭不同情况排列数为
,因此三人圆桌吃饭不同情况排列数为![]() 。
。
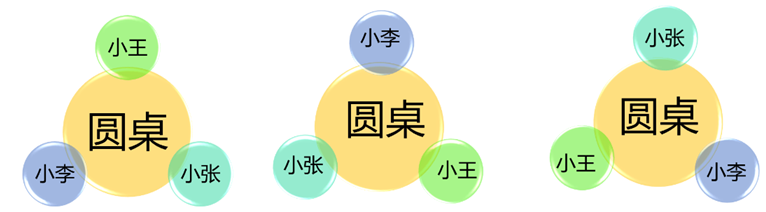
图1